DENVER – How fast can you solve this math problem:
(1 + 2) x SqRt(345.6) ÷ 78.9?
That question was the point at issue recently in a “Great Math Race” at the Space Sciences Laboratory of the University of Denver. The participants in the Math Race–it was actually a controlled experiment to compare different computational techniques – were asked to race through that problem (and several others like it). One contestant got the answer, accurate to seven decimal points, in less than 30 seconds.

There were three contenders in the Math Race, each having a different level of mathematical expertise. One was Dr. Elizabeth Tuttle, a professor in the university’s Physics and Engineering department, who regularly employs such exotic math techniques as differential equations and regression analysis in her teaching. The second was Jeff Singh, a senior mathematics major who has done advanced work in computer modeling and Numerical Methods, a specialized discipline that seeks the fastest ways to solve complex problems. The third contestant was Mac Reid, a 7-year-old second grader at South Street Elementary School whose class is currently learning how to add and subtract two-digit numbers.
The contestants were given a series of problems and asked to solve them as quickly and precisely as they could. As it happened, the race turned out the same way on each problem.
The second-grader won every time.
For the problem cited above, the math major took four minutes, forty seconds and came up with an answer of .7068. The engineering professor solved the problem in just over one minute, rounding the answer to .707. The second-grader produced a precisely accurate answer – .7068562 – in 28 seconds.
How could this happen? I wish I could report that the results were due to the winner’s inherent genius, because the second-grader in this experiment was my son.

In fact, though, truth-in-journalism requires the admission that each of the contestants used different tools in the race–and therein lies the explanation of this mathematical mystery.
The math major arrived at his answer using a No. 2 pencil and a pad of paper. He relied only on the basic arithmetic skills that everyone learns in grade school. (He computed the square root by the Newton-Rafeson iterative method, a centuries-old formula that involves repeated addition and division.) The professor attacked the problem with a slide rule–a Post Versalog dual root-scale slide rule, which provided relatively swift answers with moderate accuracy. The second-grader used a Casio ML-90 five-function electronic calculator. With that palm-sized, 2.6 ounce plastic package which cost $15 and uses 12 thousandths of a watt of electricity, the child was able to compute rings around two highly-trained mathematicians using more traditional tools. In effect, the results of the Great Math Race crystallized the computational revolution that has swept the world in the decade or so since digital electronic devices, like my son’s little calculator, came into common use.
But to attribute the second-grader’s victory to the calculator is merely to replace one mystery with another. The child’s secret weapon was a calculator; but what was the calculator’s secret weapon? How did the calculator arrive at the answer? And how did it get there so fast?
To many, probably most, of the people who use digital devices every day, the answers to these questions seem deep, inaccessible secrets. You push the keys on your calculator. The answer shows up on the screen. What happens in between is magic.
But it need not be. The calculator’s “magic” really involves a series of straightforward mathematical and logical techniques which are implemented by simple electronic switches. And these basic principles apply to all digital devices, from my son’s $15 pocket calculator to the $150 logic board that controls a Pac-Man game to the $150 million bank of computers that steers NASA’s space probes through the solar system. All these devices use the same basic parts to perform the same basic operations over and over again.
For all the mystique surrounding computers, the techniques of digital problem-solving involve simple math–considerably simpler than the stuff my son is learning in second grade. Computers approach every problem like a child counting on his fingers–except the computer counts as if it only had one finger. That’s why the machines are called “digital”–the Latin noun digitus means “a finger”. The people who design computers, video games, etc. have to manipulate this minimal skill so the machines can carry out complex operations.
The computer, in short, is a mindless simpleton–but it is a very fast mindless simpleton. Digital devices can do nothing but addition problems, and they can only add two numbers, 0 and 1. But they can do that thousands, even millions of times every second. Taking advantage of that ability, some very smart humans have taught these very dumb machines a special kind of math and a special kind of logic that permits a computer’s speed to make up for its simplicity. To understand how a computer gets the answer, then, you have to understand four basic principles of computer operation:
- Digital math
- Digital logic
- Simplicity
- Speed
DIGITAL MATH – Digital clocks, calculators, computers, and all other digital devices are made of long chains of electronic switches that work like the light switch on your wall. The switches can be either on or off; there’s nothing in between. Since there are only two possible conditions, a computer has to turn every job, every decision, every computation into the simplest possible terms–on or off, stop or go, yes or no, one or zero. Humans can do the same thing, of course; they do it on Easter morning when the kids look for hidden eggs and their parents provide only two possible clues: “You’re hot” or “You’re cold.” Eventually the eggs are found, but the process is so tedious that even the kids get tired of it pretty quickly. Computers, in contrast, use this tedious system all day, every day-because they can’t handle anything else.
Although digital devices can recognize only two numbers–one and zero–they can arrange those two to represent any number in the universe. To understand how that’s done, we’ll leave numbers for a moment and talk about words. Specifically, let’s consider the word “cat.”
Anyone who has studied a foreign language knows that there is nothing inherent in the purring, four-footed feline species that requires it to be represented by the three Roman letters C, A, and T. You can spell the thing gato or chatte and it is still the same animal. You can give it a name in Japanese kana or Chinese characters and it is still the same. The word “cat” is just a convenient symbol that English speakers have settled on for representing this object.
The same principle applies to numbers. There’s nothing inherent in the number 125, for example, that requires it to be represented by the symbols “1”, “2”, and “5.” We just happen to use that representation because of the way our number system works. Our system uses ten different symbols, or digits, for numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. To represent numbers larger than nine, we could invent more symbols. But we don’t; we rely instead on positional notation, in which each digit has a particular value based on its position. In the number 125, for example, the first (farthest right) digit represents ones, the middle digit tens, and the left-hand column hundreds. If you add up 5 ones, 2 tens, and 1 hundred you get 125. We could, of course, devise a numerical alphabet with 26 different symbols, or 125 different symbols, or 5,000 different symbols. The base-ten, or decimal, system we use is just a convenient method that people have settled on for representing all numbers.
If you want to know why the human race settled on a base-ten number system, just spread out your hands and count the digits. All creatures develop a number system based on their basic counting equipment; for humans, that means our ten fingers. (The ancient Babylonians, who counted on their two arms as well as their ten fingers, devised a base-12, or duodecimal, number system that still lives today in the methods we use to tell time and buy eggs.) Although the point is not made clear in the movie, it is a safe bet that the inhabitants of E.T.’s planet use a base-eight number system, because they have four fingers on each hand.
A computer’s basic counting equipment is simpler: it is an electronic switch that can be either on or off. If you let each of these two conditions represent one digit–if on represents one and off represents zero–you have a base-two, or binary, number system. Just as people can count to any number in the universe with just ten digits, a computer can count to any number with just two. Like people, computers do this with positional notation. In a binary number, the first (far right) column represents one, the second twos, the third fours, the fourth eights, the fifth sixteens, and so on. Thus the binary number 1111101 represents, from the right, one 1, no 2s, one 4, one 8, one 16, one 32, and one 64. If you add it up you’ll find that “1111101” is precisely the same number represented by “125” in the decimal system. The quantity hasn’t changed; the only thing that’s different is the alphabet, or number system, used to represent it.
Except for somebody who lost nine fingers in an accident, a number system based on one and zero is not particularly useful for humans. But it is, of course, perfectly suited to digital machines–so much so that the words “binary” and “digital” have become synonyms in common usage. Digital math reduces every possible number to a combination of one-or-zero, on-or-off. So, if you want to represent 125 in the circuitry of a computer, for example, you just line up seven switches this way:
ON ON ON ON ON off ON
1 1 1 1 1 0 1
Similarly, if you take 26 different off-and-on combinations and make each one a code for a letter of the alphabet, digital devices can be used to process words as well as numbers.
Binary, or digital, math is useful for computers not only because it permits switches to represent numbers. It is also the simplest mathematical system there is. In my son’s second grade class, the students have to learn math in the decimal number system; that means they have to master dozens and dozens of “math facts” – facts like 2+2=4, 9+7=16, etc. If the second-graders used the binary number system, things would be much easier. With only two numbers, there are only three math facts: 0+0=0, 1+0=1, and 1+1=10. (Remember: 10 is the binary version of the decimal number 2.)
DIGITAL LOGIC – It was human genius, of course, that figured out how to use the binary system to turn an inert chain of electronic switches into a powerful computational tool. But the inventive computer pioneers who worked out these basic arrangements didn’t stop with mathematics. They also designed a complete system of binary, or digital, logic that permits machines to make decisions and thus work through complex patterns, or “programs” of number and word processing without the need for human guidance.
Which modern high-tech genius developed this logic system? None. The binary logic that all digital devices employ today was worked out about 100 years b.c. (before computers) by a British mathematician named George Boole.
One of the great intellectual passions of Victorian England was a desire to develop a grand synthesis of all human thought. Boole devoted his life to this cause; he completed the task in 1854 and published his findings under the title “An Investigation of the Laws of Thought.” “The design of the following treatise,” he wrote at the beginning of the book, “is to investigate the fundamental laws of those operations of the mind by which reasoning is performed…and upon this foundation to establish the science of Logic.”
Boole’s central thesis was that all human reasoning could be reduced to a series of yes-or-no decisions. Each of the basic patterns of decision-making could then be represented in algebraic terms. Like many visionaries, Boole was generally ignored in his own day. (One of the few contemporaries to pay attention was another logician, Lewis Carroll, who sprinkled his “Alice” books with allusions to Boole’s ideas.) Boole died in 1864, still trying to persuade a skeptical world that his “Boolean algebra” had value.
The narrative now leaps ahead to the 1930’s and across the Atlantic to the Massachusetts Institute of Technology, where engineers were struggling to design the first primitive versions of a digital computer. It was clear that the machine could handle information in only two states–off or on, yes or no, one or zero. How could complex calculations be reduced to such simplistic patterns? An MIT grad student named Claude Shannon, who was working on the fringes of the computer-project, happened upon a copy of Boole’s book, and something clicked. In a master’s thesis published in 1938, Shannon demonstrated that yes-or-no patterns so laboriously developed by George Boole could be replicated with chains of on-or-off switches.
Shannon’s proposal was quickly adopted, and Boolean algebra has been the key to digital machines ever since. Once Boole’s ideas became important, naturally, academicians draped them in all sorts of complicated language, symbols, and formulas. At the core, though, Boolean logic is the stuff of everyday life.
You wake up from a sound sleep. If your clock says YES, it’s after 8:00, and your calendar says YES, it’s a weekday, then YES, you have to get up and go to work. If either of these conditions is a NO, however, you can stay in bed. This decision is what Boole called an AND operation. The result is yes only if condition 1 AND condition 2 are both yes.
The kitchen sink represents another basic Boolean pattern. If no faucet is on, no water comes out of the spigot. But if either the hot faucet OR the cold OR both is on, then yes, water will flow. This decision–the result is YES if condition 1 OR condition 2 OR both are YES – is what George Boole called an OR operation. Digital logic reduces all decision-making to a half-dozen basic operations like these.
Claude Shannon’s master’s thesis, which gave birth to a new discipline called “Switching Theory,” showed how electrical switches – with off representing NO and on meaning YES –could be wired together in patterns that duplicated each of the Boolean operations. The simplest AND pattern, for example, could be constructed from three switches. If current flowed into both of the two input switches–so that both switch 1 AND switch 2 were on – then switch 3 would turn on and current would flow out of it. That is, current would flow out of the 3-switch combination only if the AND operation resulted in a decision of YES. Since these switch arrangements serve to stop or pass an electric current, they are called “gates.” Every modern computer is an amalgam of AND gates, OR gates, and gates that perform each of the other digital logic operations.
SIMPLICITY – The real miracle of computers, then, is that the people who design the machines have discovered how to carry out extremely complex tasks and extremely difficult computations on a device that recognizes only two numbers – one and zero – and two logical states – yes and no. To do so, computer engineers rely on one basic design principle: simplicity. All computer operations have to be reduced to the simplest level – so simple as to seem absurd to anyone who is accustomed to human reasoning.
Consider, for example, how a calculator carries out one of its simplest tasks: you hit the “2” key and the number “2” lights up on the display screen. There’s a central switchboard inside every digital machine (the experts call this a “central processing unit” or “control unit,” but it works like an operator at a switchboard). When you press the key, the keyboard sends an electronic pulse to the switchboard operator. The following electronic “conversation” ensues:
Switchboard: Has a key been pushed?
Keyboard: Yes
S: Are you sure?
K: Yes.
S: Was it the “OFF” key?
K: No.
S: Was it a function key?
K: No.
S: Was it a number key?
K: Yes.
S: Have I asked yet if it was the “1” key?
K: No.
S: Was it the “1” key?
K: No.
S: Have I asked yet if it was the “2” key?
K: No.
S: Was it the “2” key?
K: Yes.
Eureka! After all that rigmarole (actually, much more than that; the conversation was simplified here to save space), the switchboard has finally figured that you pushed the “2.” Now the operator sends a pulse on to the display unit, and an equally laborious conversation takes place between switchboard and display screen. After 200 or so of these yes-and-no exchanges (the experts call them “instruction cycles”), the calculator finally manages to move the “2” from keyboard to screen.
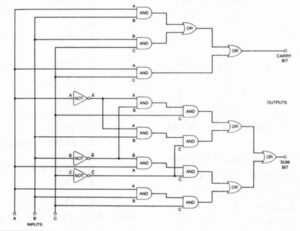
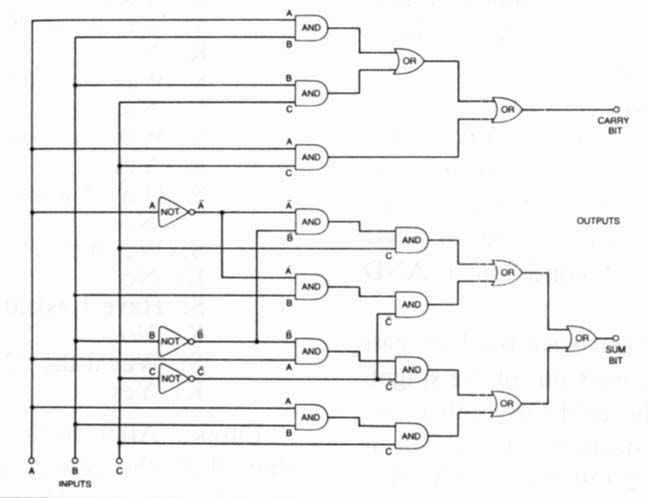
The computer’s extremely limited talents require even greater feats of virtuosity from human designers to make the machine perform mathematical computations. It is possible to design electronic logic gates that will carry out each of the four basic mathematical functions. But those gates become so huge and complicated that most of the world’s computers reduce every computation to a single function: addition. Using a mathematical trick called ones-complement subtraction (a trick that’s only possible with binary numbers), the computer can solve subtraction problems by adding. Multiplication is performed the way humans did it before they developed the multiplication table–by repeated addition. If you ask your computer to multiply 4×1,000 – a problem my son and his fellow second-graders can solve in a single mental step – the switchboard will put a binary 4 into the adding unit and then proceed to add 999 more 4s, one at a time, to get the answer. Division, similarly, becomes a series of repetitive ones-complement subtractions.
The computer user, of course, never sees any of this Byzantine complexity. If you ask your machine to compute 4×1,000, the answer comes up instantaneously. At least, it seems instantaneous – but that’s an optical illusion. The computer is quicker than the eye.
SPEED – Electronic pulses move about the circuitry of a computer, turning switches on and off in series as the logic patterns demand. These electronic signals move fast. Indeed, they move at the fastest velocity that is possible in our universe: the speed of light.
Electromagnetic radiations, including light and electronic signals, travel about 186,000 miles per second. This is quite fast, of course, but it is not the same thing as instantaneous movement.
Let’s say a New York Mets fan turns on his TV in Manhattan to watch the big game against the Dodgers in Los Angeles. The electronic signals carrying sound and picture to his TV take about .016 seconds to travel the 3,000 miles from Los Angeles to New York. Because of the signal’s transit time, the viewer sees everything about 1/62 of a second after if actually happened.
If the various parts of a computer were 3,000 miles apart, then, it would take a full second to complete every 62 steps, or instruction cycles. A simple arithmetic calculation that requires 6,200 individual steps in the computer would take 100 seconds to complete. At that rate, the machines wouldn’t win any math races. But, in fact, the parts of a computer are not miles, or feet, or even inches apart.
A quarter-century ago, when computer circuits were built with thousands of switches individually wired together, the transit time for signals moving through all that wire – miles of it in some big computers – was a significant factor that limited the machine’s computational speed. Since it was physically impossible to make the signals travel faster, computer engineers focused on giving them shorter distances to travel. The result was the integrated circuit, in which thousands of switches are jammed onto a chip of silicon about a quarter-inch square. The distance between switches today is measured in thousandths of an inch. Signals moving at the speed of light can traverse those minute distances in very short periods of time.
Indeed, the real limiting factor on computer speed is no longer the transit time for signals moving from switch to switch. The hang-up now is the time it takes for a switch to change from on to off. The computer is a long, long chain of switches; each switch has to wait for the one ahead of it to flip one way or the other before it can do anything. Thus, each switch’s switching time (the experts call this “propagation delay”) is an important performance characteristic in all modern digital tools.
“Propagation delay” is familiar to anyone who’s driven on an expressway during rush hour. If 500 cars are proceeding bumper-to-bumper and the first car stops, all the others stop as well. When the first driver puts his foot back on the accelerator, the driver in the second car sees the brake lights ahead of him go off, and he, in turn, switches his foot from brake to accelerator. The switching action is then relayed down the line of traffic. Even if each driver has a switching time from brake to accelerator of just one second, the last car in line will have to wait 500 seconds – about 8-1/2 minutes – because of the propagation delay down the line.
The electronic switches in a computer go from brake to accelerator – from on to off – somewhat faster. In the most high-powered machines, the switching time is one nanosecond–one billionth of a second. By those standards, my son’s pocket calculator is a tortoise. Its switches each take about 100 nanoseconds to go from on to off. Another way to say that is that each switch can go from on to off, from binary one to binary zero, about 10 million times each second.
There are some calculator operations that require 10 million separate steps. If you ask your calculator to take the cube root of a four-digit number, you’ll see a blank screen for a second or so while the circuit works step by step through the math. Most problems take fewer steps, though; once the computation time gets down to a quarter-second or so (2.5 million steps), the operation look instantaneous to the human eye.
You get a solid appreciation of how fast digital devices perform their logical operations if you play a video game, like Pac-Man. When the Pac-Man character is caught by a monster, it is a Boolean AND operation that destroys the Pac-Man. A computer inside the game divides the screen into several thousand individual points, each identified by its own binary number. A control unit, or switchboard, sends pulses to interrogate each point thousands of times every second. “Is Pac-Man there?” “Is a monster there?” When any point sends back a “yes” signal in reply to either query, the binary number representing that point is fed to the input of an AND gate. If the Pac Man’s location AND a monster’s location are the same, the AND gate turns on and power flows to the display switches that make Pac-Man wither and die, to the sound synthesizer that emits Pac-Man’s death whine, and to the logic gates that move a new Pac-Man into place so the game can start anew. This operation involves each of the four basic principles of digital operation: binary numbers are manipulated through digital logic that involves simple, yes-or-no steps carried out an enormous speed.
To implement the digital math and logic in practical ways, you need a switch that is small, reliable, power-efficient, and fast.
The device that meets all those criteria is a tiny piece of silicon called a transistor. It’s a switch that responds to an incoming electronic pulse by turning (depending on how its wired) either on or off. When William Shockley, John Bardeen, and Walter Brattain invented the transistor in 1947, the groundwork was laid for the modern digital computer. A decade later, when Jack Kilby and Robert Noyce invented the integrated circuit – with thousands of transistors and other electronic components integrated onto a single piece of silicon – all the clocks and games and calculators and computers that we know today became possible.
Indeed, all the parts and plans and patterns that make digital devices work were developed by a computer that is far more miraculous than any electronic machine – the human mind. It’s an obvious point, but one that seems to be forgotten sometimes as we push ahead into the cybernetic age. It was the human mind that developed all the machine-made wonders of the modern era. And it was the human mind that won, indirectly, the Great Math Race.
©1982 T. R. Reid
T. R. Reid, national reporter on leave from the Washington Post, is investigating the U.S. semiconductor industry.