On the July 4 weekend of 1981, while many Americans were preoccupied with barbecues or fireworks displays, players of an immensely complex, futuristic war game called Traveller gathered in San Mateo, California, to pick a national champion. Guided by hundreds of pages of design rules and equipment specifications, players calculate how to build a fleet of ships that will defeat all enemies without exceeding an imaginary defense budget of one trillion credits.
To design just one vessel, some fifty factors must be taken into account: how thick to make the armor, how much fuel to carry, what type of weapons, engines, and computer guidance system to use. Each decision is a tradeoff: a powerful engine will make a ship faster, but it might require carrying more fuel; increased armor provides protection but adds weight and reduces maneuverability.
Since a fleet may have as many as 100 ships–exactly how many is one more question to decide–the number of ways that variables can be juxtaposed is overwhelming, even for a digital computer. Mechanically generating and testing every possible fleet configuration might, of course, eventually produce a winner, but most of the computer’s time would be spent blindly considering designs that are nonsense. Exploring Traveller’s vast “search space,” as mathematicians call it, require the ability to learn from experience, developing heuristics–rules of thumb–about which paths are most likely to yield reasonable solutions.
In 1981, Eurisko, a computer program that arguably displays the rudiments of such skills, easily won the Traveller tournament, becoming the top-ranked player in the United States and an honorary Admiral in the Traveller navy. Eurisko had designed its fleet according to principles it discovered itself–with some help from its inventor, Douglas B. Lenat, an assistant professor in Stanford University’s artificial-intelligence program.

“I never did actually play Traveller by hand,” Lenat said, three years later. “I don’t think I even watched anybody play it. I simply talked to people about it and then had the program go off and design a fleet…When I went into the tournament that was the first time that I had ever played the game.”
Eurisko’s fleet was so obviously superior to those of its human opponents that most of them surrendered after the first few minutes of battle; one resigned without firing a shot.
Eurisko makes its discoveries by starting with a set of elementary concepts, given to it by a human programmer. Then, through a process not unlike genetic evolution, it modifies and combines them into more complex ideas. As structures develop, the most useful and interesting ones-judged according to standards encoded in the program-survive.
At the time of the Traveller tournament, Lenat had already used a forerunner of Eurisko to grow mathematical concepts, getting the program to rediscover arithmetic and some theorems in elementary number theory. Now the structures Lenat wanted to see evolve were Traveller fleets. He provided the program with descriptions of 146 Traveller concepts, some of them as basic as Acceleration, Agility, Weapon, Damage, and even Game Playing and Game. Others were more specific: Beam Laser, Meson Gun, Meson Screen, and Computer Radiation Damage.
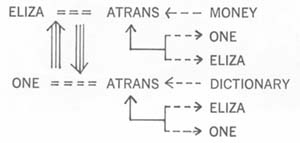
A Eurisko concept can be thought of as a box containing “slots” filled with information describing it. For example, the “Is A” slot in the box representing Energy Gun indicates that it is a Defensive Weapon Type and an Offensive Weapon Type–and a Physical Game Object, as well. These concepts are, in turn, described by other boxes. Another slot tells Eurisko that information on Energy Gun’s firing range will be found in a box called Energy Gun Attack Info.

With a network of these boxes interlinked in its memory, Eurisko began designing ships and simulating battles. After each altercation, it analyzed the results, made adjustments to the fleets and tried the battle again. In the process, Eurisko tested Traveller concepts by natural selection. For example, after a number of battles, Eurisko discovered how easy it was to provide ships with enough armor to protect them against energy guns. Thus the value in the Worth slot of Energy Gun, which was originally set at 500, was eventually lowered to 100. Weapons that proved more valuable would increase in worth, toward a maximum value of 1000.
Gradually an ever-more-invincible Traveller fleet evolved.
“At first,” Lenat later wrote, “mutations were random. Soon, patterns were perceived: more ships were better; more armor was better; smaller ships were better; etc. Gradually, as each fleet beat the previous one…its lessons were abstracted into new specific heuristics.”
When Eurisko began its experiments, the My Creator slot in each of its concepts all contained the name Lenat. But, as Eurisko played, an increasing number of the slots were filled with the name of the heuristic that had been used to synthesize them.
Eurisko was creating concepts on its own. It was distilling thousands of experiences into the judgmental, almost intuitional, knowledge that constitutes expertise–rules that can’t always be proved logically, that can’t guarantee a correct answer, but that are reliable guides to the way the world works, a means of cutting through complexity and chaos.
Each night, Lenat would leave Eurisko running on a personal computer in his office, returning in the morning to read the results, occasionally helping the process by encouraging the conjectures that seemed most fruitful and weeding out mistakes.
“Thus the final crediting of the win should be about 60/40% Lenat/Eurisko,” he wrote, “though the significant point here is that neither party could have won alone. The program came up with all the innovative designs and design rules…and recognized the significance of most of these. It was a human observer, however, (the author) who appreciated the rest, and who occasionally noticed errors or flaws in the synthesized design rules which would have wasted inordinate amounts of time before being corrected by Eurisko.”
After weeks of experimentation, and some 10,000 two-to-thirty-minute battles, Eurisko came up with what would be the winning fleet. To the humans in the tournament, the program’s solution to Traveller must have seemed bizarre. Most of the contestants squandered their trillion-credit budgets on fancy weaponry, designing agile fleets of about twenty lightly armored ships, each armed with one enormous gun and numerous beam weapons.
Eurisko, however, had judged that defense was more important than offense, that many cheap, invulnerable ships would outlast fleets consisting of a few high-priced, sophisticated vessels. There were ninety-six ships in Eurisko’s fleet, most of which were slow and clumsy because of their heavy armor. Rather than arming them with a few big, expensive guns, Eurisko chose to use many small weapons.
In any single exchange of gunfire, Eurisko would lose more ships than it destroyed, but it had plenty to spare. The first battle in the tournament was typical. During four rounds of fire, the opponent sank fifty of Eurisko’s ships, but it lost nineteen–all but one-of its own. With forty-six ships left over, Eurisko won.
Even if an enemy managed to sink all Eurisko’s sitting ducks, the program had a secret weapon–a tiny, unarmed extremely agile vessel that was, Lenat wrote, “literally unhittable by any reasonable enemy ship.” The usefulness of such a ship was discovered during a simulated battle in which a lifeboat remained afloat round after round, even though the rest of the ships in the fleet had been destroyed. To counter opponents using the same strategy, Eurisko designed another ship equipped with sophisticated guidance computer and a giant accelerator weapon. Its only purpose was killing enemy lifeboats.
After Eurisko prevailed so easily, the tournament’s directors tried to ensure that the 1982 championship would be different.
“They changed the rules significantly and didn’t announce the final new set of rules until a week or so before the next tournament,” Lenat said. “The first year that would have not been enough time for me to run the program to converge on a winning fleet design.” But Eurisko had learned heuristics that were general and powerful enough that they could be applied to new versions of the game.
“We won again and they were very unhappy and they basically asked us not to compete again. They said that if we entered and won in 1983 they would discontinue the tournaments. And I had no desire to see that happen.” So Eurisko retired undefeated.
Lenat became interested in machine intelligence while he was a student at the University of Pennsylvania. In the course of earning undergraduate and masters degrees in physics and mathematics, he began to find the abstractions becoming so rarefied that they seemed at times irrelevant.
“I got far enough in mathematics to decide that I wanted something to do that had more contact with the real world,” he said. “Also it became clear that I would not be the absolute best mathematician in the world, and that was pretty depressing…As far as physics went, I was very interested in high-energy physics and in astrophysics and general relativity. I got far enough in each case to see, again, in some ways how far from reality, how mathematical and stylized each activity was.”
Then in 1971 Lenat took a course called Introduction to Artificial Intelligence. He was immediately enthralled.
“I decided this was the place that I wanted to spend the next twenty or fifty years. What could be more exciting than figuring out how intelligence works and testing your hypotheses and theories by doing experiments to get programs to act intelligently?”
In 1972 Lenat went to Stanford University, one of the major centers of artificial-intelligence research. His early doctoral work was in automatic programming–the attempt to design software that, given a simple description of a task to be computerized, will write an appropriate program. Designing good software is such an intricate, time-consuming process that making programs write programs is expected to eventually create yet another revolution in the computer industry. Meanwhile, research in automatic programming is providing insight into how an intelligent system–whether natural or artificial–can analyze a problem and solve it by devising a plan.
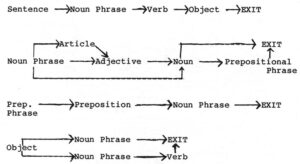
Much of the early work in artificial intelligence, a discipline that has only existed since the late 1950s, was based on the assumption that the best way to get a computer to solve problems is to teach it logic. Suppose a program was to figure out how to get a robot to retrieve a book from the top of a table. First the problem was coded into symbolic logic. Some axioms described the initial situation: On(Book, Table), At(Table, X), At(Robot, Y), meaning that the book is on the table, the table is at place X, and the robot is at place Y.
Since computers don’t come with world-views ready made, nothing can be taken for granted. Simple rules, such as the fact that if an object is at place X and it is moved to place Y, then it will be at place Y, had to be translated into still more axioms. Then the problem to be solved (getting the robot to the book) was described as a theorem-At(Robot, Book)–which the computer had to prove by deriving it from the axioms using rules of logic. In the process of construction the proof, a plan for moving the robot would emerge as a byproduct.
But using logic to solve even the simplest problems turned out to be very difficult. To find a correct proof for a theorem, the computer had to juxtapose axiom after axiom, searching for the proper constellation. Problems involving more than a few axioms generated enormous search spaces. If the number of axioms were doubled, the number of possible configurations squared; triple the axioms and the configurations cubed. When the plan to be produced was as complex as a computer program, this “exponential explosion” was especially severe. By the time Lenat arrived at Stanford, researchers had realized that in automatic programming the search space was too vast to negotiate without heuristics that captured some of the programmer’s art.
While some researchers began working on ways to use heuristics to guide the theorem-proving method, Lenat became interested in a less formal, more human-like approach. He began by imagining a group of experts sitting in a room and collaborating on writing a program. He imagined how many experts would be necessary to write a program, what each would have to know and say to the others, how tasks would be delegated. Then he wrote a program called Beings, in which the experts were imitated by sections of computer code.
“There was one subroutine called Psychologist and one subroutine called Loop Expert and one subroutine called Domain Expert, and so forth,” Lenat said. “There were maybe a hundred of these little beings altogether. You’d post a problem and one of them would recognize it and broadcast to the whole community a set of requests for what needed to get done in order to solve it. And anyone who–any being who could recognize any of those requests would respond to it, process it, and broadcast requests of what it needed to have done…That succeeded pretty well…One of the tasks we applied the program to was synthesizing Patrick Winston’s thesis.”
For his doctoral dissertation, Winston, who now heads the artificial intelligence laboratory at the Massachusetts Institute of Technology, wrote a program–one of the classics in the field–that could learn to recognize simple block configurations, like arches. After being presented with samples of what is and is not an arch, the program would construct an internal model of the concept and use it to judge future examples.
First, Lenat wrote the dialogue his beings would engage in if they were writing Winston’s program. (The beings included one called User, the human running the program, who could be called on occasionally to supply information or resolve disputes.)
“For each Being we had a list of the very specific facts that it needed to know. And I coded them up and now we had this system that carried out the original dialogue perfectly. Each expert that was just the right expert came in at just the right time–it was spectacular, and, sure enough, Winston’s thesis program came out as the end product. And it was great–except it couldn’t do anything else.”
The program’s knowledge was too specific to apply to other tasks.
“Of all the 500,000 things that a psychologist might know we only put down that it had to know the ten things that it had to know in order to do Winston’s thesis program. And so if you asked anything else, and a psychologist should have responded, this one wouldn’t, because it didn’t know that. And so I was very depressed because on the one hand I’d succeeded with this massive goal, but on the other hand I hadn’t really learned anything. And the reason was that having a very specific target, knowing where you want to go, makes it too easy to get there…So I said, Okay, let’s try and design a program that doesn’t know where it’s going…And the idea of mathematics research came to me as the archetypal case where you’re playing around with concepts and you don’t really have any particular goal in mind…And so I said, Okay, fine, we’ll write down ahead of time all the knowledge that’s reasonable to know to guide a researcher in elementary mathematics. And then we’ll set the program loose and we won’t add to it or do anything to it and just see where it goes, and that will be the experiment.”
Lenat called his new program AM, for Automated Mathematician. For the next several months he coded into it knowledge about set theory, a very abstract and basic discipline that forms the infrastructure of mathematics. A set is simply a collection of objects(A,B,C,D), for example. It doesn’t matter what the letters represent: rocks, cars, people, galaxies. A set is an abstraction, and set theory is the science describing the behavior of this pure mindstuff.
For AM to understand set theory it had to know about such fundamental notions as equality (when two sets are identical), union (when two sets are combined to form a third set) and intersection (when the members that two sets have in common are used to form a third set). Lenat included 115 such concepts in AM, along with several hundred heuristics that captured some of the rudiments of mathematical discovery and aesthetics. One heuristic, for example, said that a good way to start exploring a concept is to find examples of it. Another said that if a concept has few examples, try creating a new, more general version of it.
Guided by such rules, AM conducted hundreds of experiments in set theory, modifying and combining ideas until new ones evolved like crystals growing in a supersaturated solution. In this way, the program chanced upon the concept of natural numbers, which enabled it to discover arithmetic. The concept of union led to that of addition; addition led to multiplication, which led to exponentiation.
One heuristic advised AM to study the inverse of interesting functions. Thus, AM turned multiplication into the concept of divisors. By applying a heuristic that suggested looking for extreme examples, it found numbers that have only two divisors: the primes. Once AM knew about primes it was only a matter of time before it created versions of such famous mathematical ideas as Goldbach’s conjecture (every even number greater than two is the sum of two primes) and the fundamental theorem of arithmetic: any number can be factored into a unique set of primes.

“AM went off and discovered hundreds of things,” Lenat said, “about half of which were useful and half of which were sort of weird and probably losers.” But, after its first 200 discoveries, AM began to run dry.
“It started doing silly things, one after another, like defining numbers that were both odd and even…or other just awful stuff that doesn’t exist, or of which there is only one.” The percentage of good concepts–the “hit rate,” as Lenat called it–dropped from 62.5% to less than 10%.
As the conceptual world AM was building grew increasingly complex, Lenat realized, the heuristics he had provided it were becoming inadequate. They had been written to deal with sets, not arithmetic and number theory. To test his hypothesis, Lenat added some new heuristics, raising the hit rate slightly.
Then he had an insight that led to the invention of Eurisko: Heuristics, like any other concept, could be coded in the system as boxes with slots. By giving the program access to its own heuristics, it could experiment with them, gathering data, analyzing pattems-helping them evolve to keep pace with the expanding conceptual realm. Heuristics could be applied to heuristics. The rules about when to specialize or generalize mathematical concets, or when to raise or lower their worth, or combine them to form new ideas-all could be applied to this new domain of learning how to make better discoveries.
When AM was accepted as Lenat’s doctoral dissertation in 1976, he was already at work on Eurisko.
So far, the program’s most profitable success has been in Traveller, but Lenat has found his system to be general enough to make discoveries-and discoveries about discoveries-in many domains. When loosed upon the field of microscopic circuitry design, Eurisko discovered a new configuration for a memory cell, which might, however be of limited use since, Lenat wrote, “the cell can be realized most efficiently on the surface of a Mobius strip.” By giving Eurisko a set of concepts about LISPthe language in which it is written-it was able to modify parts of itself to make them more efficient.
But as with any program, there are always bugs to work out. Sometimes a “mutant” heuristic appears that does little more than continually cause itself to be triggered, creating within the program an infinite loop. During one run, Lenat noticed that the number in the Worth slot of one newly discovered heuristic kept rising, indicating that Eurisko had made a particularly valuable find. As it turned out the heuristic performed no useful function. It simply examined the pool of new concepts, located those with the highest Worth values, and inserted its name in their My Creator slots.
It was a heuristic that, in effect, had learned how to cheat.
©1984 George Johnson
George Johnson, a freelance writer, is reporting on the quest to build computers smarter than humans.